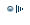Основные законы:

Отрицание логического высказывания — логическое высказывание, принимающее значение"истинно", если исходное высказывание ложно, и наоборот.Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания. 
Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности. 
Алгоритм построения таблицы истинности: 
1. Подсчитать количество переменных n в логическом выражении.
2. Определить число строк в таблице, которое равно m = 2n.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице: количество переменных + количество операций = количество столбцов.
4. Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов.
5. Заполнить стобцы входных переменных наборами значений.
6. Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Составление ТИ по логической схеме. По своей структуре выражение, описывающее релейный автомат, совпадает с логикой алгебры высказывания.