Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составного высказывания, не вникая в их содержание.

Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно или ложно.

В алгебре высказываний простым высказываниям ставятся в соответствии логические переменные, обозначаемые прописными буквами латинского алфавита. 

Например:
А= “Листва на деревьях опадает осенью”.
В= “Земля прямоугольная”.

Высказывания, как говорилось уже ранее, могут быть истинными или ложными. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0.

Например:
А=1
В=0
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истинна” (1) и “ложь” (0).

В алгебре высказываний над высказываниями можно производить логические операции, в результате которых получаются новые, составные (сложные) высказывания.

Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.

Логическая операция	Название	Соответствует союзу	Обозначение знаками	Таблица истинности	Логическая операция
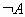
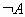
Инверсия  (от лат. inversion – переворачиваю)	отрицание	не А		A 1 0 0 1	Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Конъюнкция  (от лат. conjunction – связываю)	Логическое умножение	А и В		A B 1 1 1 1 0 0 0 1 0 0 0 0	Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны
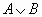
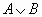
Дизъюнкция  (от лат. disjunction – различаю)	Логическое сложение	А или В		A В 1 1 1 1 0 0 0 1 0 0 0 0	Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
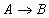
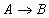
Импликация  (от лат. implication – тесно связывать)	Логическое следование	Если А,  то В; Когда А, тогда В	А–условие В-следствие	A В 1 1 1 1 0 0 0 1 0 0 0 1	Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие.
Эквивалентность (от лат. equivalents - равноценность)	Логическое равенство	А тогда и только тогда, когда В		A В 1 1 1 1 0 0 0 1 0 0 0 1	Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны